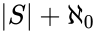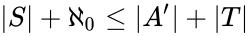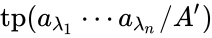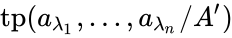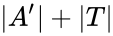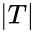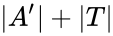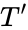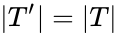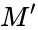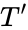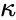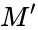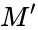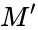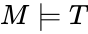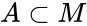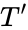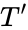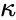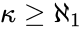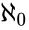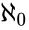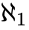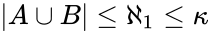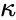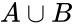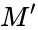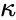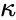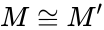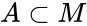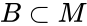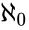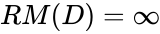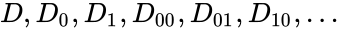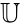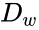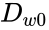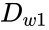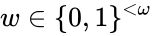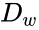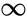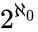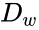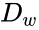The Ehrenfeucht-Mostowski construction is a construction which produces models in which few types are realized.
Theorem. Let  be a complete theory with infinite models. Then for any
be a complete theory with infinite models. Then for any 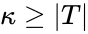 , there is a model
, there is a model 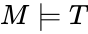 of cardinality
of cardinality 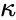 such that if
such that if 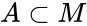 , then at most
, then at most  types over
types over  are realized.
are realized.
Proof. First suppose that  has definable Skolem functions. Let
has definable Skolem functions. Let 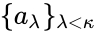 be a non-constant indiscernible sequence of length
be a non-constant indiscernible sequence of length 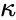 in some model
in some model 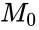 . We can find such an indiscernible sequence by extracting an indiscernible sequence from a non-constant sequence in an infinite model. Let
. We can find such an indiscernible sequence by extracting an indiscernible sequence from a non-constant sequence in an infinite model. Let  be
be 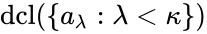 . Because
. Because  has definable Skolem functions,
has definable Skolem functions,  , so
, so 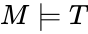 and
and 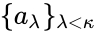 is still indiscernible within
is still indiscernible within  . The set
. The set 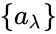 is called the spine. Let
is called the spine. Let  be a subset of
be a subset of  . Each element of
. Each element of  is in the definable closure of some finite subset of the spine, so we can find some
is in the definable closure of some finite subset of the spine, so we can find some  contained in the spine, with
contained in the spine, with 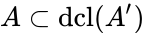 , and
, and 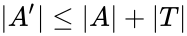 . An element’s type over
. An element’s type over  is determined by its type over
is determined by its type over  , because
, because 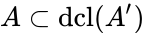 . So it suffices to show that at most
. So it suffices to show that at most 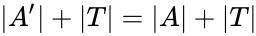 types over
types over  are realized.
are realized.
First we check that at most 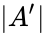 types are realized by tuples from the spine. We can write
types are realized by tuples from the spine. We can write  as
as 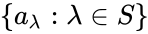 for some
for some 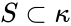 with
with 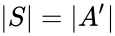 . The indiscernibility of the spine implies that
. The indiscernibility of the spine implies that 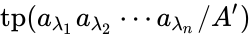 is entirely determined by how the
is entirely determined by how the 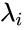 relate to each other and how they relate to elements of
relate to each other and how they relate to elements of 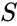 . That is,
. That is, 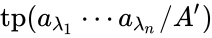 is entirely determined by the following pieces of data:
is entirely determined by the following pieces of data:
- Whether
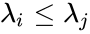 for each
for each 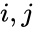 .
.
- The set
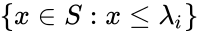 for each
for each  .
.
- The set
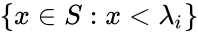 for each
for each  .
.
Because 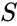 is well-ordered, there are only about
is well-ordered, there are only about 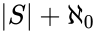 choices for the second and third bullet points. All told, there are therefore only
choices for the second and third bullet points. All told, there are therefore only 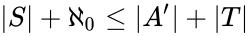 possibilities for
possibilities for 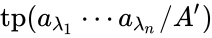 .
.
Now if  is a 0-definable function, then
is a 0-definable function, then  depends only on
depends only on 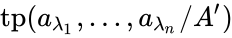 , so there are at most
, so there are at most 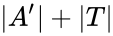 types over
types over  realized by elements of the form
realized by elements of the form  . But all of
. But all of  is in the definable closure of the spine, so every element of
is in the definable closure of the spine, so every element of  is of this form. Since there are only
is of this form. Since there are only 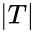 -many 0-definable functions, the total number of types over
-many 0-definable functions, the total number of types over  realized in
realized in  is at most
is at most  So at most
So at most 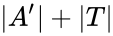 types over
types over  are realized, completing the proof (in the case where we had definable Skolem functions).
are realized, completing the proof (in the case where we had definable Skolem functions).
Now suppose  is arbitary. We can find a theory
is arbitary. We can find a theory 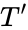 expanding
expanding  , which does have Skolem functions. This can easily be done in such a way that
, which does have Skolem functions. This can easily be done in such a way that 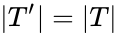 . By the above argument one gets a model
. By the above argument one gets a model 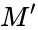 of
of 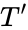 of size
of size 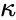 with the property that for every subset
with the property that for every subset  of
of 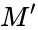 , at most
, at most  types over
types over  are realized in
are realized in 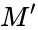 . Let
. Let  be the reduct of
be the reduct of 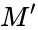 to the original language. Then
to the original language. Then 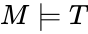 . If
. If 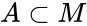 , and
, and  and
and  have the same
have the same 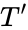 -type over
-type over  , then they certainly have the same
, then they certainly have the same  -type over
-type over  within
within  , because
, because  has fewer definable sets and relations to work with than
has fewer definable sets and relations to work with than 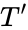 . So there are at most as many
. So there are at most as many  -types over
-types over  as there are
as there are 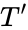 -types over
-types over  , which is at most
, which is at most  . QED
. QED
An important consequence of this result is the following, which is the first step of the proof of Morley’s Theorem.
Corollary. Let  be a complete countable theory which is
be a complete countable theory which is 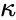 -categorical for some
-categorical for some 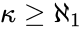 . Then
. Then  is
is 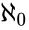 -stable (hence totally transcendental).
-stable (hence totally transcendental).
Proof. Let 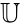 be the monster model of
be the monster model of  . Suppose
. Suppose  is not
is not 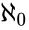 -stable. Then we can find a countable set
-stable. Then we can find a countable set  over which there are uncountably many types. Realize
over which there are uncountably many types. Realize 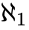 of these types and let
of these types and let  be the set of these realizations. Then
be the set of these realizations. Then 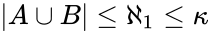 , so by Löwenheim-Skolem we can find a model
, so by Löwenheim-Skolem we can find a model  of cardinality
of cardinality 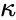 containing
containing 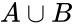 . By the Ehrenfeucht-Mostowski construction, we can find a model
. By the Ehrenfeucht-Mostowski construction, we can find a model 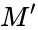 of cardinality
of cardinality 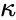 in which at most countably many types are realized over countable sets. By
in which at most countably many types are realized over countable sets. By 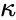 -categoricity,
-categoricity, 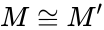 . So
. So  also has the property that over countable sets, countably many types are realized. But over the countable set
also has the property that over countable sets, countably many types are realized. But over the countable set 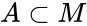 , uncountably many types are realized in
, uncountably many types are realized in 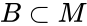 , a contradiction.
, a contradiction.
(It is a general fact that 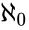 -stable theories are totally transcendental. The proof goes as follows: if
-stable theories are totally transcendental. The proof goes as follows: if  failed to be totally transcendental, then
failed to be totally transcendental, then 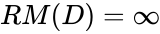 for some set
for some set 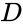 . Then one inductively builds a tree
. Then one inductively builds a tree 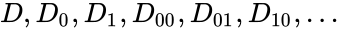 of non-empty
of non-empty 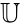 -definable sets such that
-definable sets such that 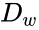 is the disjoint union of
is the disjoint union of 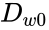 and
and 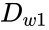 for every
for every 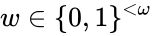 , and such that each
, and such that each 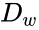 has Morley rank
has Morley rank 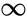 . This is the same construction used to prove that perfect sets in Polish spaces have cardinality
. This is the same construction used to prove that perfect sets in Polish spaces have cardinality 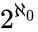 . At any rate, there are countably many
. At any rate, there are countably many 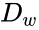 ’s, so the
’s, so the 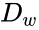 ’s are all definable over some countable set
’s are all definable over some countable set  . Now each path through the tree yields a different type over
. Now each path through the tree yields a different type over  , so that there are uncountably many types over
, so that there are uncountably many types over  , contradicting
, contradicting 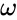 -stability.) QED
-stability.) QED
 be a complete theory with infinite models. Then for any
be a complete theory with infinite models. Then for any  , there is a model
, there is a model 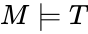 of cardinality
of cardinality 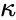 such that if
such that if 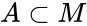 , then at most
, then at most  types over
types over  are realized.
are realized.

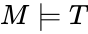
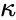
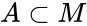



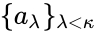
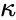
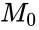

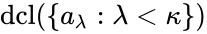


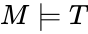
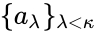

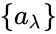




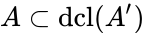
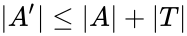


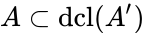
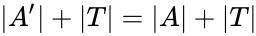

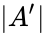

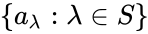
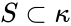
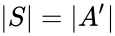
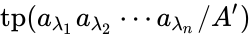
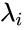
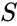
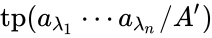
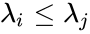 for each
for each 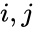 .
.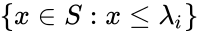 for each
for each  .
.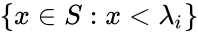 for each
for each  .
.