SCF is the theory of separably closed fields. So a field  is a model of SCF if every polynomial
is a model of SCF if every polynomial ![{\displaystyle P(X)\in K[X]}](https://wikimedia.org/api/rest_v1/media/math/render/png/8fbf6a56e7c4b31f7f192187a9b38112399a9faa) whose roots in
whose roots in 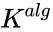 are distinct, has at least one root in
are distinct, has at least one root in  . Equivalent conditions are that every irreducible polynomial over
. Equivalent conditions are that every irreducible polynomial over  is of the form
is of the form  where
where 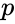 is the characteristic, or that the perfect closure of
is the characteristic, or that the perfect closure of  is algebraically closed. In characteristic zero, SCF is the same as ACF. So one usually restricts to the case of positive characteristic.
is algebraically closed. In characteristic zero, SCF is the same as ACF. So one usually restricts to the case of positive characteristic.
If  is a separably closed field of characteristic
is a separably closed field of characteristic 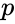 , then
, then 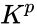 (the set of
(the set of 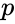 th powers) is a subfield of
th powers) is a subfield of  . The degree of the extension
. The degree of the extension 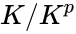 is
is 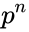 , where
, where  is a number called the degree of imperfection. The degree of imperfection of the separable closure of
is a number called the degree of imperfection. The degree of imperfection of the separable closure of 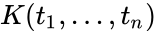 is
is  , if
, if  is an algebraically closed field of characteristic
is an algebraically closed field of characteristic 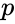 . It turns out that models of SCF are determined up to elementary equivalence by their characteristic and degree of imperfection (as an element of
. It turns out that models of SCF are determined up to elementary equivalence by their characteristic and degree of imperfection (as an element of 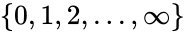 ).
).
All models of SCF are stable, and the non-algebraically closed ones are strictly stable, i.e., not superstable.
SCF does not have quantifier elimination in the language of rings. However, it does have quantifier elimination or model completeness in a language where one names a "p-basis" and adds "lambda functions." Basically, it turns out that if  has degree of imperfection
has degree of imperfection  , then one can find elements
, then one can find elements  such that the set of monomials of the form
such that the set of monomials of the form  is a vector space basis of
is a vector space basis of  over
over 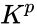 . Then each element
. Then each element 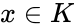 has a unique expression of the form
has a unique expression of the form 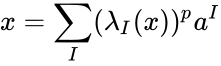 where
where 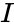 ranges over multiindices in
ranges over multiindices in 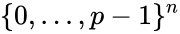 . After naming the elements of a
. After naming the elements of a 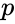 -basis, the
-basis, the 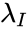 's become definable functions from
's become definable functions from  to
to  , and it turns out that after adding symbols for them, one has quantifier elimination, or maybe just model completeness.
, and it turns out that after adding symbols for them, one has quantifier elimination, or maybe just model completeness.
When the degree of imperfection is infinite, something more complicated must be done.
Separably closed fields played a key role in Hrushovski's proof of Geometric Mordell Lang in positive characteristic.
 is a model of SCF if every polynomial
is a model of SCF if every polynomial ![{\displaystyle P(X)\in K[X]}](https://wikimedia.org/api/rest_v1/media/math/render/png/8fbf6a56e7c4b31f7f192187a9b38112399a9faa) whose roots in
whose roots in 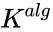 are distinct, has at least one root in
are distinct, has at least one root in  . Equivalent conditions are that every irreducible polynomial over
. Equivalent conditions are that every irreducible polynomial over  is of the form
is of the form  where
where 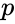 is the characteristic, or that the perfect closure of
is the characteristic, or that the perfect closure of  is algebraically closed. In characteristic zero, SCF is the same as ACF. So one usually restricts to the case of positive characteristic.
is algebraically closed. In characteristic zero, SCF is the same as ACF. So one usually restricts to the case of positive characteristic.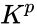 (the set of
(the set of 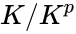 is
is 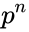 , where
, where  is a number called the degree of imperfection. The degree of imperfection of the separable closure of
is a number called the degree of imperfection. The degree of imperfection of the separable closure of 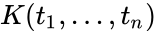 is
is 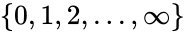 ).
). such that the set of monomials of the form
such that the set of monomials of the form  is a vector space basis of
is a vector space basis of 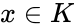 has a unique expression of the form
has a unique expression of the form 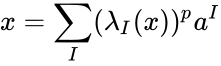 where
where 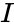 ranges over multiindices in
ranges over multiindices in 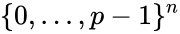 . After naming the elements of a
. After naming the elements of a 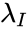 's become definable functions from
's become definable functions from