 with an endomorphism
with an endomorphism 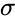 . The theory of difference fields is inductive, and ACFA is its model companion. Therefore, models of ACFA are existentially closed difference fields.
. The theory of difference fields is inductive, and ACFA is its model companion. Therefore, models of ACFA are existentially closed difference fields.A difference field is a field 
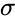
ACFA can be explicitly axiomatized as follows. 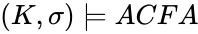
 is an algebraically closed field
is an algebraically closed field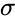 is an automorphism of
is an automorphism of  , in particular, it is surjective
, in particular, it is surjective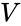 is an irreducible affine variety over
is an irreducible affine variety over  , and if
, and if 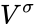 is the image of
is the image of 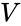 under
under 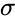 , and if
, and if 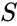 is an irreducible closed subvariety of
is an irreducible closed subvariety of 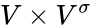 such that the projection maps
such that the projection maps 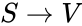 and
and 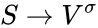 are dominant, and if
are dominant, and if  is a proper closed subvariety of
is a proper closed subvariety of 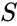 , then there is some
, then there is some 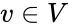 such that
such that 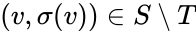 .
.The fact that this third condition is first-order is a little non-trivial, and uses the fact that irreducibility is definable in ACF.
ACFA is supersimple, but not stable. It is probably one of the most important examples of a simple unstable theory. ACFA has elimination of imaginaries. ACFA does not have quantifier elimination, but comes very close.
A model 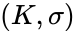
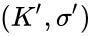
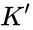
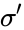
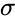

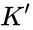
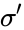
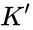
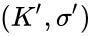
The upshot is that the completions of ACFA are in bijection with pairs 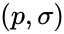
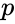
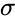
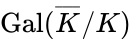

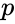
ACFA does not have quantifier elimination. However, every formula is equivalent to one of the form 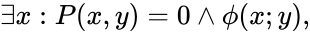

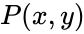

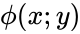
If 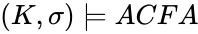
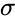
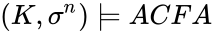

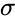
In the unpublished paper The Elementary Theory of the Frobenius, Hrushovski proves that ACFA is the limit theory of the Frobenius automorphism, in the same sense that the theory of pseudo-finite fields is the limit theory of finite fields.
More precisely, for each prime power 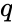
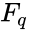
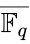
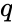
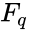
Some analogue of the Zilber Trichotomy holds in ACFA (which is unstable). This was proven by Chatzidakis and Hrushovski, maybe, at least in the characteristic 0 case.
As an application, this can be used to give yet another proof of the Manin-Mumford conjecture.
Hrushovski's result on the elementary theory of the frobenius has been used to prove results in algebraic dynamics about periodic points, by Fakhruddin and someone else.
Also, the trichotomy in ACFA has been used by Medvedev and Scanlon to prove results in algebraic dynamics, about periodic varieties.